左のように一つの閉回路ができる接続方法をΔ接続といいます。
右のような回路の接続方法をY接続といいます。
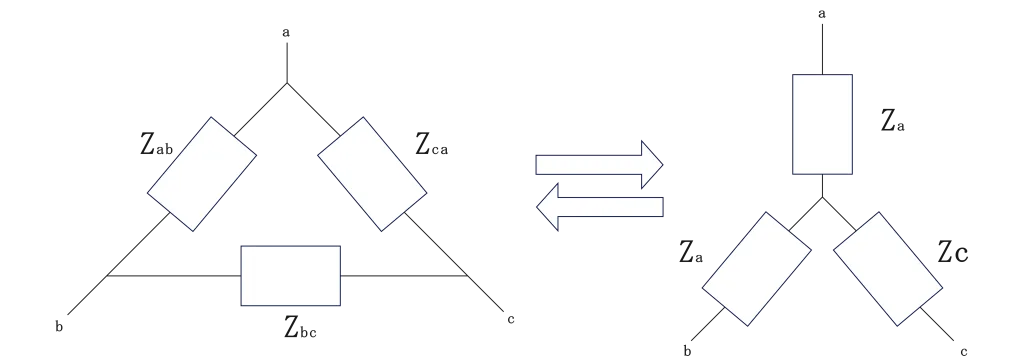
今回はΔ接続からY接続、Y接続からΔ接続の変換方法について説明していきます。
Y-Δ変換
まず、ΔからYに変換できるということは、例えば点a-b間の電圧、インピーダンス、電流は等価であるということです。
Δ回路で点a-b間のインピーダンスを考えると、\(Z_{ab}\)と\(Z_{bc}+Z_{ca}\)の合成インピーダンスなので
\(Z_{ab}//(Z_{bc}+Z_{ca})=\frac{Z_{ab}(Z_{bc}+Z_{ca})}{Z_{ab}+Z_{bc}+Z_{ca}}\)
同様にb-c,c-a間のインピーダンスはそれぞれ、
\(Z_{bc}//(Z_{ab}+Z_{ca})=\frac{Z_{bc}(Z_{ab}+Z_{ca})}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{ca}//(Z_{ab}+Z_{bc})=\frac{Z_{ca}(Z_{ab}+Z_{bc})}{Z_{ab}+Z_{bc}+Z_{ca}}\)
また、Y回路のa-b,b-c,c-a間のインピーダンスはそれぞれ、
\(Z_{ab}=Z_a+Z_b\)
\(Z_{bc}=Z_b+Z_c\)
\(Z_{ca}=Z_c+Z_a\)
Y-Δはそれぞれインピーダンスは等価なので、a-b,b-c,c-a間は以下の等式が成り立ちます。
\(Z_{ab}=Z_a+Z_b=\frac{Z_{ab}(Z_{bc}+Z_{ca})}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{bc}=Z_b+Z_c=\frac{Z_{bc}(Z_{ab}+Z_{ca})}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_{ca}=Z_c+Z_a=\frac{Z_{ca}(Z_{ab}+Z_{bc})}{Z_{ab}+Z_{bc}+Z_{ca}}\)
ここで、計算を楽にするために\(S=Z_{ab}+Z_{bc}+Z_{ca}\)と置くと、
\(\begin{cases}Z_a+Z_b=\frac{Z_{ab}(Z_{bc}+Z_{ca})}{S}\\Z_b+Z_c=\frac{Z_{bc}(Z_{ab}+Z_{ca})}{S}\\Z_c+Z_a=\frac{Z_{ca}(Z_{ab}+Z_{bc})}{S}\end{cases}\)
\(Z_a+Z_b=α,Z_b+Z_c=β,Z_c+Z_a=θ\)とすると
\(α+θ-β=2Z_a,α+β-θ=2Z_b,β+θ-α=2Z_c\)
これを整理すると
\(Z_a=\frac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_b=\frac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_c=\frac{Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
Δ-Y変換
\(Z_a=\frac{Z_{ab}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_b=\frac{Z_{ab}Z_{bc}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
\(Z_c=\frac{Z_{bc}Z_{ca}}{Z_{ab}+Z_{bc}+Z_{ca}}\)
を用いると、
\(Z_{ab}=Z_a+Z_b+\frac{Z_aZ_b}{Z_c}=\frac{Z_aZ_b+Z_bZ_c+Z_aZ_c}{Z_c}\)
\(Z_{bc}=Z_a+Z_b+\frac{Z_bZ_c}{Z_c}=\frac{Z_aZ_b+Z_bZ_c+Z_aZ_c}{Z_b}\)
\(Z_{ca}=Z_a+Z_b+\frac{Z_cZ_a}{Z_c}=\frac{Z_aZ_b+Z_bZ_c+Z_aZ_c}{Z_c}\)
このようにしてY-Δの変換を行うことができます。


コメント